SPOJ 8002 HORRIBLE

www.spoj.com/problems/HORRIBLE/

Este problema puede ser resuelto usando un Segment Tree con lazy updates. En cada nodo almacenaremos la suma de los valores de los nodos hijos, y al recibir una operación de incremento vamos a usar lazy updates para actualizar solo los nodos que serán consultados.

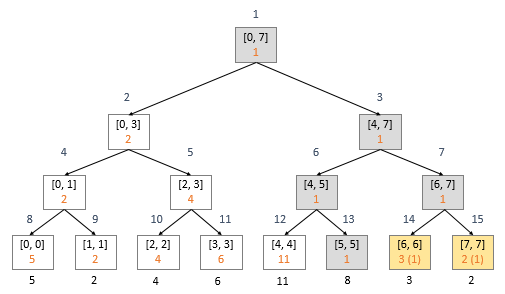
La forma de aplicar lazy updates en este problema consiste en almacenar una variable en cada nodo con el valor con el que deben ser actualizados. Al actualizar un intervalo, agregamos a esta variable el incremento × (r-l+1) donde [l, r] es el intervalo que representa el nodo. De esta manera, el nodo queda actualizado temporalmente como si hubieran sido actualizados todos sus nodos hijos. Hay que cuidar de esto en las operaciones merge y split de cada nodo.

Mi codigo del Segment Tree para este problema:

static class SegmentTree
{
    int N;
    Node[] tree;
    class Node
    {
        public int start, end;
        public long sum, add;

        public Node(int l, int r){ start = l; end = r; }

        public void merge(Node l, Node r)
        {
            if (l == null) sum = r.sum + r.add * (r.end - r.start + 1);
            else if (r == null) sum = l.sum + l.add * (l.end - l.start + 1);
            else sum = l.sum+l.add*(l.end-l.start+1) + r.sum+r.add*(r.end-r.start+1);
        }

        public void split(int l, int r)
        {
            sum += add * (end - start + 1);
            if (end != start)
            {
                Node leftChild = tree[l]; leftChild.add += add;
                Node rightChild = tree[r]; rightChild.add += add;
            }
            add = 0;
        }
    }

    public SegmentTree(int[] A)
    {
        N = A.length;
        int power = (int) Math.floor(Math.log(A.length) / Math.log(2)) + 1;
        int len = (int) Math.pow(2, power);
        tree = new Node[len];
        build(1, 0, A.length-1, A);
    }

    private void build(int node, int l, int r, int[] A)
    {
        if (l == r)
        {
            tree[node] = new Node(l, r);
            tree[node].sum = A[l];
            return;
        }
        int nL = node << 1, nR = nL + 1, mid = (l + r) >> 1;
        build(nL, l, mid, A);
        build(nR, mid + 1, r, A);
        tree[node] = new Node(l, r);
        tree[node].merge(tree[nL], tree[nR]);
    }

    public void update(int i, int j, int val) { update(1, 0, N - 1, i, j, val); }

    private void update(int node, int l, int r, int i, int j, int val)
    {
        int nL = node << 1, nR = nL + 1, mid = (l + r) >> 1;
        if (i <= l && j >= r)
        {
            tree[node].add += val;
            tree[node].split(nL, nR);
            return;
        }
        if (j < l || i > r) return;
        update(nL, l, mid, i, j, val);
        update(nR, mid + 1, r, i, j, val);
        tree[node].merge(tree[nL], tree[nR]);
    }

    public long query(int i, int j) { return query(1, 0, N - 1, i, j).sum; }

    private Node query(int node, int l, int r, int i, int j)
    {
        int nL = node << 1, nR = nL + 1, mid = (l + r) >> 1;
        if (l >= i && r <= j)
        {
            if (tree[node].add > 0) tree[node].split(nL, nR);
            return tree[node];
        }
        if (j < l || i > r) return null;
        if (tree[node].add > 0) tree[node].split(nL, nR);
        Node a = query(nL, l, mid, i, j);
        Node b = query(nR, mid + 1, r, i, j);
        Node temp = new Node(-1, -1);
        temp.merge(a, b);
        return temp;
    }
}

Segment Trees II: lazy updates

Cambiar todos los elementos en un intervalo

Esta operación se puede realizar en O(log n) usando una técnica conocida como lazy updates (actualizaciones perezosas). Esta técnica básicamente actualiza solo los nodos que necesitamos en ese momento, y pospone las demás actualizaciones para el momento en que sean necesarias. Para esto utilizaremos la operación split.

Para llevar a cabo esta operación  el intervalo que queremos actualizar lo marcaremos como pendiente, y en las operaciones de consulta es donde realmente se actualizara el intervalo, propagando las marcas de actualización de un nodo a sus hijos, y actualizando solamente el valor del nodo padre. De esta forma, solo actualizaremos en realidad los nodos que sean consultados, y los que no sean consultados, se quedarán marcados como pendientes. Para esto necesitaremos cambiar un poco la clase Node, y las operaciones de update y query.

class Node
{
    boolean flag;
    int left, right, value, updated;
    public Node (int l, int r)
    {
        left = l; right = r;
    }
    public void merge (Node leftChild, Node rightChild)
    {
        if (leftChild == null) value = rightChild.value;
        else if (rightChild == null) value = leftChild.value;
        else value = Math.min(leftChild.value, rightChild.value);
    }
    public void split(int nL, int nR)
    {
        if (left != right) // marcar los hijos
        {
            Node leftChild = tree[nL];
            leftChild.flag = true;
            leftChild.updated = updated;
            Node rightChild = tree[nR];
            rightChild.flag = true;
            rightChild.updated = updated;
        }
        flag = false;
        value = updated;
    }
}

Utilizaremos la variable flag para marcar los nodos como pendientes, y el método split para propagar las actualizaciones a los hijos de los nodos que han sido marcados. El método para actualizar el intervalo se encarga de marcar los nodos.

private void update(int node, int l, int r, int i, int j, int v)
{
    int leftChild = 2*node, rightChild = leftChild+1, mid = (l+r)/2;
    if(i <= l && j>= r)
    {
        tree[node].updated = v;
        tree[node].flag = true;
        tree[node].split(leftChild, rightChild);
    }
    else if (j < l || i > r) return;
    else
    {
        update(leftChild, l, mid, i, j, v);
        update(rightChild, mid+1, r, i, j, v);
        tree[node].merge(tree[leftChild], tree[rightChild]);
    }
}
public void update(int i, int j, int newValue)
{
    update(1, 0, N-1, i, j, newValue);
}

El método query es el que se encarga de propagar las actualizaciones por el árbol  sencillamente usando la operación de split en cada nodo que sea visitado al ejecutar la consulta.

private Node query(int node, int l, int r, int i, int j)
{
    int leftChild = 2*node, rightChild = leftChild+1, mid = (l+r)/2;
    if (l >= i && r <= j)
    {
        if (tree[node].flag) tree[node].split(leftChild, rightChild);
        return tree[node];
    }
    if (j < l || i > r) return null;
    if (tree[node].flag) tree[node].split(leftChild, rightChild); // nodo visitado
    Node a = query(leftChild, l, mid, i, j);
    Node b = query(rightChild, mid+1, r, i, j);
    Node temp = new Node(N, N);
    temp.merge(a, b);
    return temp;
}
public int query(int i, int j)
{
    Node result = query(1, 0, N-1, i, j);
    return result.value;
}

De esta forma las operaciones de actualización son propagadas por el árbol  Por ejemplo, si actualizáramos el intervalo [5, 7] a 1 en el arreglo original [5, 2, 4, 6, 11, 8, 3, 2] la secuencia de operaciones seria la siguiente:

1. comenzamos en la raíz [0-7]
   1. hijo izquierdo [0-3] esta fuera del intervalo, retornar.
   2. hijo derecho [4-7] esta parcialmente dentro, visitar sus hijos.
      1. hijo izquierdo [4-5] esta parcialmente dentro, visitar sus hijos.
         1. hijo izquierdo [4-4] esta fuera, retornar.
         2. hijo derecho [5-5] esta completamente dentro. Marcar como pendiente y hacer split. Se actualiza su valor, y no se propaga porque no hay hijos.
         3. actualizar el valor de [4-5] usando merge. El valor ahora es 1.
      2. hijo derecho [6-7] esta completamente dentro. Marcar como pendiente y hacer split. Se marcan sus hijos como pendientes, y se actualiza el valor a 1.
      3. actualizar el valor de [4-7] usando merge. El valor ahora es 1.
   3. actualizar el valor de [0-7] usando merge. El valor ahora es 1.

Nodos modificados en la operación de actualización

En la figura se puede ver el resultado de la operación anterior. Los nodos marcados en gris fueron actualizados en la operación. Los nodos marcados en amarillo fueron marcados como pendientes y el valor entre paréntesis es el nuevo valor que tendrán después de actualizarlos. Dado que en la operación se recorre el camino de la raíz a un nodo, y luego de vuelta, la operación es O(log n). De esta forma podemos realizar de forma eficiente actualizaciones sobre un intervalo. En próximos post vamos a ver como puede ser generalizado el Segment Tree para resolver otros problemas mas complicados.

Referencias

en.wikipedia.org/wiki/Segment_tree

wcipeg.com/wiki/Segment_tree

comeoncodeon.wordpress.com/2009/09/15/segment-trees/

letuskode.blogspot.com/2013/01/segtrees.html

p–np.blogspot.com/2011/07/segment-tree.html

www.algorithmist.com/index.php/Segmented_Trees

Problemas

www.spoj.com/problems/HORRIBLE/

www.spoj.com/problems/SEGSQRSS/