Hola a todos, debido a las limitaciones de WordPress.com, he decidido comenzar un nuevo blog en sportcoder.com. El nuevo blog estara en ingles, con el objetivo de ser util a una mayor audiencia, y finalmente este blog no seguira siendo actualizado. Puedes visitar mi nuevo blog aqui.
Saludos!
Flujo Maximo
Los problemas de flujo máximo son problemas que aparecen a menudo en la vida real, como también en competencias de programación. En la forma mas común del problema, tenemos varias tuberías de agua, que están conectadas entre si y tienen distintas capacidades. Cual es la mayor cantidad de agua que se puede transportar de un punto inicial a uno final a través de estas tuberías?
En términos de teoría de grafos, nos dan una red – grafo dirigido, en la cual cada arista tiene una capacidad c asociada, y se selecciona un nodo inicial x y un nodo final y. Nuestra tarea es asignar a cada arista un valor f (f ≤ c de la arista) de manera tal que para todo nodo, la suma de f de todas las aristas que entran, sea igual a la suma de f de todas las aristas que salen. Este valor de f es llamado flujo en la arista. Mas aun, se nos pide maximizar la suma del flujo de las aristas que entran al nodo final.
Redes residuales y caminos de aumento: mas flujo
La red residual del grafo es, dicho de forma simple, el mismo grafo, con aristas duplicadas. Especificamente, si en la arista a-b del grafo original, el flujo es menor que la capacidad, en la red residual ponemos una arista de a-b con capacidad igual a la diferencia entre la capacidad y el flujo (esta es la capacidad residual). Y si en el grafo original, el flujo es mayor que cero, en la red residual ponemos una arista b-a con capacidad del flujo.
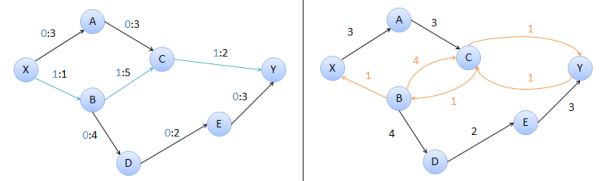
Un camino de aumento es un camino desde el nodo inicial hasta el final, con un flujo incrementado. En la imagen anterior, si consideramos el camino X-A-C-Y en la red residual, podemos incrementar el flujo en el grafo. Las aristas X-A y A-C tienen capacidad 3, pero como C-Y tiene capacidad 1, el menor de estos valores es la capacidad del camino.
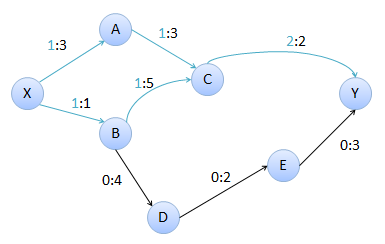
El valor del flujo total ahora es 2, pero puede ser aun mas. No tiene sentido considerar las aristas X-B ni C-Y, ya que estas estan completas, pero existe otro camino. Vamos a construir nuevamente la red residual
El único camino que hay de X a Y es X-A-C-B-D-E-Y. Este camino no existe en el grafo real, solo en la red residual ya que C-B no es una arista en el grafo original. Sin embargo, podemos usar este camino para aumentar el flujo en el grafo, y C-B sera usada como un flujo negativo en el grafo real. Una vez mas, la cantidad de flujo que podemos incrementar es 1, que es la menor de las capacidades en el camino.
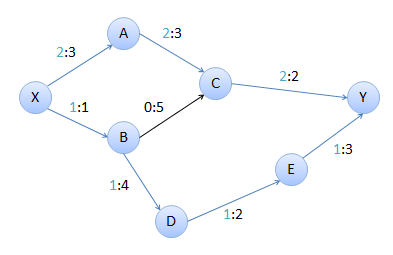
Si construimos la red residual con estos nuevos valores, encontramos que no existe ningun camino de X a Y.
Este ejemplo sugiere el siguiente algoritmo: comenzamos con cero flujo en todas las aristas, y vamos incrementando el flujo total mientras exista un camino de aumento sin aristas completas o aristas invertidas vacias, esto es: un camino en la red residual. De hecho, este es el algoritmo encontrado por Ford y Fulkerson y publicado en 1956.
Algoritmo de caminos de aumento: Ford-Fulkerson
La forma general del algoritmo seria asi (pseudocodigo)
function maxflow
result = 0
while (true)
// encontramos un nuevo camino
pathCapacity = findPath()
// no se encontro ninguno
if (d = 0) exit
else result += pathCapacity
return result
Este algoritmo siempre llega a una solucion correcta, sin importar como busquemos los caminos de aumento. Sin embargo, cada camino de aumento podria incrementar el flujo en solo 1 unidad, por tanto el numero de iteraciones podria ser muy grande si escogemos un metodo poco eficiente para buscar los caminos de aumento. Tres métodos pueden ser usados:
- DFS (Depth-First Search o Buscar por Profundidad)
- BFS (Breadth-First Search o Busqueda por Anchura)
- PFS (Priority-First Search o Busqueda por Prioridad)
De estas opciones, DFS es la mas sencilla de implementar, pero tiene menor eficiencia que los otros métodos. BFS es la implementacion mas común, ya que es relativamente simple de implementar y siempre encuentra el camino de aumento mas corto entre la fuente y el destino.
Implementando con BFS
Supongamos que tenemos las capacidades de las aristas en una matriz C[x, y]. En el algoritmo con BFS, vamos a buscar el camino mas corto entre la fuente y el destino y calcular la minima capacidad de las aristas en el camino – la capacidad del camino. Posteriormente, para cada arista en el camino, reducimos su capacidad e incrementamos la capacidad de la arista invertida como mostramos anteriormente. Vamos a ver el pseudocodigo.
int bfs()
queue Q
meter fuente en Q
marcar fuente visitado
// mantenemos el arreglo from, donde from[x] es el nodo anterior
// en el camino de la fuente a x
inicializar from con -1 (valor sentinela)
while Q no vacio
u = sacar de Q
para todo vertice v adyacente a u
if v no visitado y C[u][v] > 0
meter v en Q
marcar v visitado
from[v] = u
if v = destino
terminar while
fin para todo
fin while
// calculamos la capacidad del camino
v = destino, capacidad = infinito
while from[v] > -1
u = from[v] // vertice anterior
capacidad = mininmo(capacidad, C[u][v])
v = u
fin while
// actualizamos la capacidad residual si se encontro el camino
v = destino
while from[v] > -1
u = from[v]
C[v][u] -= capacidad
C[u][v] += capacidad
v = u
fin while
// si no hay camino, capacidad es infinito
if capacidad = infinito
return 0
else
return capacidad
En cuanto a eficiencia, el peor caso del algoritmo de flujo seria en total O(N×M2), pero usualmente el algoritmo se comporta mejor que esto. Esta implementacion con BFS es conocido como el algoritmo de Edmonds-Karp.
Implementando con PFS
En este caso se busca siempre el camino con mayor capacidad de aumento. A simple vista, esto podría mejorar el algoritmo ya que en cada paso se aumenta el flujo en la mayor cantidad posible, pero en algunos grafos el método de BFS tiene mejores tiempos. Para implementar este método, la prioridad asignada a cada vértice es la menor capacidad en el camino de la fuente al vértice. Procesamos cada vértice en una manera golosa, como en el algoritmo de Dijkstra, de mayor a menor prioridad. Cuando lleguemos al destino, terminamos, ya que se encontró el camino con la mayor capacidad. Este algoritmo lo debemos implementar con una estructura que nos permita encontrar el vértice con mayor prioridad, e incrementar su prioridad de forma eficiente. Esta estructura es un heap o cola con prioridad.
Vamos a ver como implementarlo con el pseudocodigo.
int pfs()
priority queue PQ
meter node(source, infinity, -1) en PQ
mantenemos from como en el BFS
// si no hay camino de aumento, path_cap es 0
path_cap = 0
while PQ no vacia
aux = sacar de PQ
u = aux.vertex, cost = aux.priority
si ya visitamos u continuamos
from[u] = aux.from
if u = sink
path_cap = cost
salir de while
marcar u visitado
para todo vertice v adyacente a u
if C[u][v] > 0
new_cost = min(cost, C[u][v])
meter node(v, new_cost, u) en PQ
fin para todo
fin while
// actualizar red residual
v = destino
while from[v] > -1
u = from[v]
C[u][v] -= path_cap
C[v][u] += path_cap
v = u
fin while
return path_cap
El análisis de este método es un poco mas complicado, pero con esta implementacion el algoritmo de flujo seria O(M×logN×F), donde M es la cantidad de aristas, N es la cantidad de vértices y F es el flujo máximo en el grafo. Aunque este algoritmo parece ser mas eficiente, en la practica los dos se comportan de forma similar. Cual escoger a la hora de codificar es un asunto de preferencia, aunque el método de BFS es mas sencillo.
Referencias
http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=maxFlow
http://en.wikipedia.org/wiki/Max_flow
http://jason-kok.appspot.com/algorithm/network
Boyer-Moore-Horspool
Un problema muy común es, dado un texto, encontrar la posición de una palabra dada en el texto. Existen varios algoritmos que resuelven este problema de una forma eficiente, aunque la eficiencia de cada algoritmo esta condicionada por varios factores del texto, como el tamaño del alfabeto, el largo del texto, y del patrón, etc. Uno de los algoritmos mas famosos para resolver este problema es el algoritmo de Boyer-Moore. Este algoritmo fue modificado después por Nigel Horspool, con el objetivo de crear un algoritmo que fuera rápido al buscar en textos de alfabetos naturales (lenguajes humanos) y a la vez sencillo de entender e implementar. El algoritmo fue publicado en 1980 con el nombre de Boyer-Moore-Horspool.
El algoritmo esta basado en dos ideas fundamentales:
- Buscar de derecha a izquierda
- Calcular los saltos que se pueden hacer para avanzar mas en la búsqueda
Buscar la aguja en el pajar
Tenemos el texto ‘TEXTOGENERADOALEATORIAMENTE’, y queremos encontrar la posicion de ‘EATOR’ dentro del texto. A continuacion, nos referiremos a ‘EATOR’ como el patron, y a ‘TEXTOGENERADOALEATORIAMENTE’ como el texto.
1. Alineamos el patrón con el texto
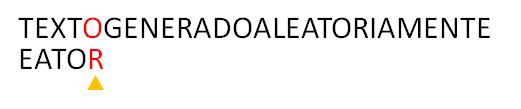
2. Comparamos de derecha a izquierda los caracteres del patrón con los del texto. En el patrón tenemos ‘R‘ y en el texto ‘O‘. En este caso, el algoritmo común movería a ciegas una posición a la derecha el patrón, en cambio, nuestro algoritmo trata de alinear el caracter del texto que esta alineado con el ultimo caracter del patron, con su posición mas a la derecha en el patrón.

3. De esta forma se alinean las dos O, y se vuelve a comparar comenzando por la derecha. Al comparar ‘R‘ con ‘G‘, el algoritmo trata de alinear ‘G‘ con su posición mas a la derecha en el patrón, pero dado que ‘G‘ no aparece en el patrón, podemos correctamente alinear el patrón hasta despues de la ‘G‘ en el texto, ya que el patron no puede aparecer antes de esa posicion, porque no contiene la ‘G‘.

4. Ahora al comparar ‘R‘ con ‘A‘, alineamos la ‘A‘ del texto con la del patrón, y se vuelve a comparar de derecha a izquierda

5. Sucede lo mismo que en el caso anterior, volvemos a alinear la ‘A‘ con su posición en el patrón

6. Idem

7. En este caso, el algoritmo continua comparando de derecha a izquierda hasta encontrar el patrón completo en el texto. Aquí tenemos una aparición.

8.En este punto el algoritmo puede terminar concluyendo que se encontró el texto en la posición dada, o continuar a buscar todas las posiciones donde aparece el patrón dentro del texto. En este caso, alinearíamos la ‘R‘ del texto a su próxima posición en el patrón, como no aparece mas, podemos mover el patrón pasada la ‘R‘ del texto.
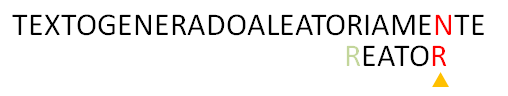
9. En este punto, al comparar ‘N‘ con ‘R‘ notamos que ‘N‘ no aparece en el patrón, y al mover el patrón pasado ‘N‘, el algoritmo termina, ya que no hay suficientes caracteres en el texto para seguir comparando.

Precalcular la aguja
Para ejecutar el algoritmo, necesitamos definir la función R, que dado un caracter c del texto, R(c) nos indica la cantidad de posiciones que debemos mover el patrón para alinear la posición mas a la derecha de c en el patrón con la posición actual de c en el texto. Esta función se puede precalcular para cada uno de los caracteres del texto, y luego usarla en el algoritmo de forma constante.
Con esta función definida, el algoritmo alinea a cada paso el patrón con la posición actual en el texto. En caso de una coincidencia, se continua explorando el patrón tratando de encontrar mas coincidencias, en caso de encontrar dos caracteres diferentes, el algoritmo usa la función R(c) en el caracter del texto que esta siendo alineado con el ultimo caracter del patrón para calcular la nueva alineación del patrón. La implementacion quedaria asi
public int[] preBoyerMooreHorspool(char[] P, char[] T, int size)
{
int pLength = P.length;
int last = P.length - 1;
// precalcular R
int[] R = new int[size];
for(int i = 0; i < size; i++) R[i] = pLength;
for(int i = 0; i < last; i++) R[P[i]] = last - i;
return R;
}
Esta función inicialmente asigna a cada letra del alfabeto (size es el tamaño del alfabeto) un salto del tamaño del patrón. Esto sucede en el caso en que la letra no aparece en el patrón. Luego, a las letras que están en el patrón (excepto la última) se le asigna un salto del tamaño de su posición más a la derecha.
El algoritmo luego va a usar la tabla para ir alineando el patrón con el texto
public int boyerMooreHorspool(String pattern, String text)
{
char[] P = pattern.toCharArray();
char[] T = text.toCharArray();
int pLength = P.length;
int offset = 0;
int scan = 0;
int last = P.length - 1;
int maxoffset = T.length - P.length;
// precalcular R
int[] R = preBoyerMooreHorspool(P, T, 256);
// aun hay suficientes caracteres para comparar
while(offset <= maxoffset)
{
// comparar de derecha a izquierda
for(scan = last; P[scan] == T[scan+offset]; scan--)
if(scan == 0) return offset; // encontrado
offset += R[T[offset + last]]; // alinear el patron
}
return -1; // no encontrado
}
En esta implementación se usa 256 para el tamaño del alfabeto. Esto se puede modificar para tamaños menores del texto, pero con la observación de que este algoritmo es particularmente eficiente para alfabetos grandes y patrones largos. Para alfabetos pequeños (como el de ADN o el binario) es mas eficiente usar la versión completa de Boyer-Moore.
Análisis
El algoritmo tiene un caso peor acotado por O(nm) donde n es el tamaño del texto y m del patrón. En la practica sin embargo – y especialmente con alfabetos de tamaño grande – este caso nunca ocurre. De hecho, el algoritmo se comporta en orden sublineal, ya que en la mayoría de las ocasiones los saltos que se producen en el algoritmo conllevan a que se produzcan pocas comparaciones. El análisis de este algoritmo es sumamente complejo, pero no es difícil notar que en el mejor caso, se realizan solamente O(n/m) comparaciones.
La siguiente gráfica muestra como se comporta el algoritmo comparado con otros algoritmos conocidos que resuelven el mismo problema:

Referencias
http://en.wikipedia.org/wiki/Boyer%E2%80%93Moore%E2%80%93Horspool_algorithm
http://www.mathcs.emory.edu/~cheung/Courses/323/Syllabus/Text/Matching-Boyer-Moore2.html
http://www.iti.fh-flensburg.de/lang/algorithmen/pattern/horsen.htm
http://www-igm.univ-mlv.fr/~lecroq/string/node18.html
http://www.cs.ucdavis.edu/~gusfield/cs224f09/bnotes.pdf
Problemas
Codeforces 311A The Closest Pair
http://codeforces.com/problemset/problem/311/A
Este es un problema interesante, porque nos pide analizar un problema ya resuelto, al contrario de resolverlo.
Haciendo un análisis del tiempo del algoritmo que presentan en el texto del problema, se puede encontrar que el for exterior se ejecuta n veces, y el interior se ejecuta (n − i) veces, si logramos que nunca ocurra el break que hay dentro.
Partiendo de esto podemos calcular que tot se incrementa cada vez que ocurre un ciclo, lo que es igual a 
Asi podemos concluir que si tot ≤ k, no existe solución posible.
De lo contrario hay que encontrar un conjunto de puntos que impidan que ocurra el break. Para esto tenemos que hacer que la sentencia d ≤ p[j].x - p[i].x sea siempre falsa. En el caso evidente, podemos seleccionar todos los puntos con la misma coordenada x, y se cumple la condición ya que d tiene que ser mayor que cero porque todos los puntos son diferentes.
Con este análisis, el código se resume a comprobar si n(n-1) > k, y mostrar n diferentes puntos con la misma x coordenada.
Mi código en Codeforces http://codeforces.com/contest/311/submission/3788135
Codeforces 289B
http://codeforces.com/problemset/problem/289/B
En problemas como estos, generalmente la primera parte de la solución es encontrar el caso donde no se puede resolver. Dado que solo podemos sumar o restar d a los elementos de la matriz, si encontramos al menos 2 elementos cuya diferencia no sea múltiplo de d, es imposible igualar esos elementos.
En el caso donde existe la solución podemos transformar un poco el problema, y convertir la matriz en un arreglo común ordenado ascendentemente. Luego de esto, la solución optima seria restar d a los números mayores y sumar d a los menores hasta llegar a un punto común donde todos los elementos sean iguales. Cual es este punto común? El elemento que esta en el centro del arreglo.
Esta es la mejor solución ya que si escogemos un valor mayor que el valor central, los elementos menores van a necesitar mayor cantidad de operaciones para igualar, y si escogemos un valor menor que el central, se necesitan mas operaciones para igualar los elementos mayores.
Despues de encontrar cual es el elemento central, la solución es la suma de |ai – c| / d para cada elemento ai en el arreglo.
Mi solucion en Codeforces http://codeforces.com/contest/289/submission/3463481
UVa 10656
http://uva.onlinejudge.org/external/106/10656.pdf
El problema pide encontrar una sub-secuencia de suma máxima. Dado que los números son no negativos, la secuencia de mayor suma es… la secuencia completa! Sin embargo, el problema especifica que si existen mas de 1, debemos seleccionar la de menor tamaño. Esto solo es posible cuando aparecen ceros en la secuencia, ya que estos no modifican la suma, y por tanto, debemos excluirlos. La solución es solo tomar todos los números en la entrada mayores que cero, e imprimirlos. En el caso en que todos los elementos son ceros, solo hay que imprimir 0.
UVa 11057
http://uva.onlinejudge.org/external/110/11057.html
Una posible solución seria iterar para cada libro disponible, si el libro tiene precio p, podemos calcular el valor M-p y buscar si tenemos otro libro con este precio, de esta manera encontramos un par de libros que son una solución. Este método es O(n^2) y dado que podemos tener hasta 10000 libros, esta solución es demasiado lenta. Sin embargo, si ordenamos inicialmente los precios de los libros, podemos aplicar una búsqueda binaria para determinar si existe el valor M-p, y de esta forma obtenemos un algoritmo O(n log n). Solo hay que tener en cuenta no escoger el mismo libro 2 veces, ya que esto no es una solución valida.
UVa 10341
http://uva.onlinejudge.org/external/103/10341.pdf
Método de Biseccion
Hay que observar que para que la función contenga una raíz en el intervalo [0, 1], los signos de f(0) y f(1) tienen que ser opuestos. Esta propiedad se puede aplicar para buscar el valor de la x. Dado un intervalo [l, r] podemos aplicar el siguiente método de bisección:
- Tomamos el valor medio entre [l, r] y lo denotamos por m.
- Calculamos f(l) y f(m). Si el signo de estos es opuestos, la raíz se encuentra en el intervalo [l, m], y podemos descartar el intervalo [m, r].
- De lo contrario, la raíz se encuentra en el intervalo [m, r] y descartamos [l, m] de la búsqueda.
Este método es muy eficiente, pero existen otras formas de calcular las raíces de una función que podemos aplicar a este problema. Tales métodos son el método de las secantes, y el método de Newton. Vamos a ver las soluciones con estos métodos:
Método de la Secante
La aplicacion de este metodo consiste en aproximar sucesivamente la pendiente de una recta a la pendiente de la funcion en un punto dado. El metodo esta dado por la relacion de recurrencia:
![]()
Lo podemos calcular iterativamente, calculando en cada paso la x actual, y cuando el valor de f(x) sea lo suficientemente aproximado a 0, termina la funcion. Una posible implementacion seria la siguiente:
public double secant(double x0, double x1, double precision)
{
while(true)
{
double delta = f(x1)*(x1 - x0) / (f(x1) - f(x0));
if (abs(delta) < precision) return x1;
x0 = x1;
x1 = x1 - delta;
}
}
Metodo de Newton
El metodo de Newton es otra forma de calcular la raiz de una funcion. Este metodo funciona de manera muy similar al metodo de la secante, pero es mas «inteligente» al aproximarse a la raiz, ya que utiliza la recta tangente a la curva, y no una aproximacion a ella. Este metodo es sumamente eficiente cuando podemos calcular la derivada de la funcion original. El metodo esta definido por la relacion
![]()
Dada la funcion f y su derivada fd, podemos calcular los valores de x iterativamente como en el metodo de la secante:
public double secant(double x, double precision)
{
while(true)
{
double delta = f(x) / fd(x);
if (abs(delta) < precision) return x;
x = x - delta;
}
}
De los tres métodos presentados, el método de Newton es el mas eficiente, ya que se acerca a la raíz de forma mas inteligente que los anteriores, sin embargo para usarlo, es necesario calcular la derivada de la función. En los casos en que no se pueda calcular, podemos usar cualquiera de los dos anteriores.
Referencias
http://es.wikipedia.org/wiki/M%C3%A9todo_de_la_secante
UVa 11935
http://uva.onlinejudge.org/external/119/11935.pdf
Supongamos que conocemos la capacidad mínima necesaria que debe tener el tanque, sea esta capacidad C, cumple la siguiente propiedad:
- toda capacidad c < C no es suficiente para llegar al destino
- toda capacidad c > C sera suficiente para llegar al destino.
Esta propiedad nos permite realizar una búsqueda binaria para encontrar el valor de C.
Comenzamos con una capacidad mínima de 0 y una máxima de 100000 es suficiente. En cada paso de la búsqueda binaria vamos a escoger el valor medio entre el máximo y el mínimo y simular los eventos del viaje con esta capacidad. Si el resultado es que no alcanza, entonces podemos descartar todos los valores menores que el, y fijar la búsqueda entre el valor del medio y el mayor valor. Si encontramos que con esa capacidad es suficiente, entonces descartamos todos los valores mayores y fijamos la búsqueda entre el valor mínimo y el valor medio.
Codeforces 274A
http://codeforces.com/problemset/problem/274/A
Dados dos numeros x, y si x = y×k, estos dos números no pueden estar en el mismo conjunto. La solución para el problema es tomar cada numero x en el conjunto de entrada, y comprobar si x/k esta presente en el conjunto, y quitar uno de los dos. Con las dimensiones del problema, tenemos que usar búsqueda binaria. Para esto necesitamos ordenar el arreglo de forma descendente, y dado que x/k es menor que x, podemos aplicar la búsqueda binaria hacia adelante. Si encontramos que este numero esta en el conjunto original, lo removemos. Finalmente, la respuesta es la cantidad de números que no fueron eliminados.
Mi solucion en Codeforces http://codeforces.com/contest/274/submission/3170587
Codeforces 276C
http://codeforces.com/problemset/problem/276/C
La solución para este problema es incluir los números mas grandes en el arreglo en las posiciones donde sean mas consultados, para que contribuyan la mayor cantidad al resultado total. Para esto hay que calcular cuales son las posiciones que mas aparecen en las consultas. Esto se puede lograr usando un BIT e introducir cada intervalo de consulta como update(l, 1) y update(r+1, -1). Luego podemos consultar en el BIT dada una posición i, cuantos intervalos contienen esa posición Ordenamos las posiciones descendentemente por la cantidad de intervalos que la contienen, y los números del arreglo en orden descendiente. Finalmente, cada numero en el arreglo original contribuye a la suma con n×T[i], donde T[i] es el valor de la cantidad de intervalos que contienen la posición i.
Existe otra forma de calcular la cantidad de intervalos que contienen una posición dada, que no requiere de ninguna estructura especial. Esto lo podemos calcular con un arreglo A[i]. Dado un intervalo [l, r], incrementamos A[l] y decrementamos A[r+1].
Después de procesar todos los intervalos, calculamos A[i] = A[1] + A[2] + … + A[i]. Dada una posición i, hay 3 casos:
- [l, r] termina antes que i. En este caso, se cancela el incremento en l con el decremento en r, y no se afecta el valor de A[i].
- [l, r] comienza después de i. En este caso, el incremento es después de la posición i, por tanto no se afecta su valor.
- [l, r] contiene a la posición i. En este caso, solo contamos el valor del incremento en l, ya que r esta después de i.
Esta técnica es mas sencilla y puede ser usada para muchos otros tipos de problemas en los que se requiera tratar con intervalos.
Mi solución en Codeforces http://codeforces.com/contest/276/submission/3203916
Codeforces 275B
http://codeforces.com/problemset/problem/275/B
Este es uno de esos problemas en los que hay que simular la solución Hay que notar que dado que solo podemos cambiar la dirección 1 vez en un camino de una celda negra a otra, solo pueden haber 2 posibles caminos entre cualquier par de celdas negras. Con las dimensiones del problema, basta chequear para todo par de celdas negras, si se puede ir por alguno de estos 2 posibles caminos, y en caso de encontrar una pareja para las que no sea posible, concluimos que es no convexo. Si es posible para todas las parejas, es convexo.
Mi solucion en Codeforces: http://codeforces.com/contest/275/submission/3174573
Árbol de Fenwick 2D
El Árbol de Fenwick (conocido también como BIT) es una estructura muy eficiente para calcular sumas en intervalos. En este post vamos a ver como podemos usarlo en un problema de dos dimensiones. El problema es el siguiente:
Supongamos que tenemos un terreno rectangular que representa un sembrado de tamaño n × m. Podemos sembrar plantas en distintos puntos de este terreno, y estamos interesados en saber cuantas plantas hay en una porción dada del terreno.
Para resolver este problema, necesitamos definir 2 operaciones:
- Consulta. Esta operación calcula, dada una porción del terreno, cuantas plantas hay dentro de esa porción.
- Actualización. Esta operación agrega una o varias plantas en una posición dada del terreno.
Estas son operaciones similares a las del BIT, pero en este caso las vamos a realizar sobre un arreglo bidimensional. Esto lo podemos hacer creando un BIT donde cada elemento del árbol, sera a su vez un BIT convencional.

Al crear un BIT 2D, podemos realizar las operaciones que necesitamos para resolver el problema. En este caso, cada elemento del BIT sera responsable por un intervalo de filas en el arreglo bidimensional, y contendrá otro BIT que sera responsable por un intervalo de columnas. Al crear un BIT 2D a partir del arreglo bidimensional, cada elemento (i, j) del arreglo almacenara la suma del rectángulo desde (0, 0) hasta (i, j).
Consultando sumas acumuladas
Con este diseño podemos responder fácilmente la suma acumulada en el rectángulo desde (0, 0) hasta (i, j). Similar al BIT convencional, vamos a recorrer los nodos responsables de las filas, y de cada nodo vamos a recorrer los responsables en el BIT que este contiene. Suponiendo que la información sea almacenada en el arreglo bidimensional T[i, j], la operación de consulta quedaría así:
public int sum(int i, int j)
{
int result = 0;
for(int r = i; r > 0; r-= lowbit(r))
for(int c = j; c > 0; c-= lowbit(c))
result+= T[r][c];
return result;
}
Esta operación es O(log n × log m), ya que recorremos los responsables en las filas, y para cada uno de ellos, los responsables en el BIT interno. Si queremos consultar la suma en un rectángulo dentro dentro del arreglo, tenemos que realizar otros cálculos.

Si deseamos calcular el valor dentro del rectángulo verde, tendríamos que calcular la suma desde la posicion (0, 0) hasta la esquina inferior derecha de este rectángulo (A) y restarle los valores acumulados en los rectángulos 1 y 2 (B y C); y sumarle el valor del rectángulo 3, ya que este esta comprendido dentro de 1 y 2 y lo restamos dos veces al quitar los valores de ellos (D).
public int sum(int i, int j, int i2, int j2)
{
int a = sum(i2, j2) + sum(i-1, j-1);
int b = sum(i2, j-1) + sum(i-1, j2);
return a-b;
}
Cambiar los valores
Para esta operación tenemos que cambiar el valor en la posición que queremos, y luego recorrer todos los nodos responsables de la fila en que se encuentra la posición, y en cada BIT contenido en la fila, actualizar los valores en los elementos responsables.
public void update(int i, int j, int v)
{
for(int r = i; r < n; r += lowbit(r))
for(int c = j; c < m; c += lowbit(c))
T[i][j] += v;
}
Esta operacion es O(log n × log m) y su analisis es similar a la operacion de consulta.
Con estas operaciones podemos resolver el problema planteado. De manera similar podemos extender el BIT a mas dimensiones, y asi resolver problemas mas complejos.
Felices codigos!
Referencias
community.topcoder.com/tc?module=Static&d1=tutorials&d2=binaryIndexedTrees
Problemas
SPOJ 6256 INVCNT
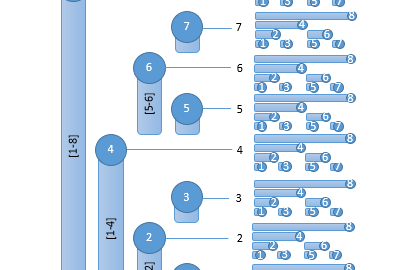
Este problema puede ser resuelto con un árbol de Fenwick. Nos dan el arreglo A como entrada. A partir de este arreglo, podemos crear un BIT de tamaño 10^7. Para cada elemento en A, vamos a insertar 1 en la posición correspondiente en el BIT.
Por ejemplo, en el primer caso, los elementos son [3, 1, 2]. Insertamos 1 en la posición 3, 1 en la 1 y 1 en la 2.
Para responder cuantas inversiones se forman, podemos consultar cada vez que insertemos un numero, cuantos mayores que el se han insertado, esto es, consultar el intervalo [n+1, 10^7] en el BIT. En el ejemplo, después de insertar 1 en 3, tenemos 0 mayores que el, ya que no se ha insertado ninguno después de 3. Al insertar 1 en 1, tenemos 1 mayor que 1, ya que el 3 fue insertado antes. Y al insertar el 2, también tenemos 1 mayor que 2. Para dar la respuesta, sumamos la cantidad de inversiones para cada numero.
UVA 11926 Multitasking
uva.onlinejudge.org/external/119/11926.pdf
Este problema puede ser resuelto usando un árbol de Fenwick, pero en una forma no convencional. Crearemos el árbol del tamaño de la máxima duración de una tarea (10^6), y lo vamos a utilizar para contar cuantas tareas se están ejecutando en un momento dado.
Cada tarea esta representada por el inicio (s) y el final (e). Supongamos que en la posición s del BIT insertamos 1. De esta manera, cuando consultemos cuantas tareas se están ejecutando en el momento s, tendremos 1. Pero dada la estructura de responsabilidades del BIT, si consultamos en cualquier momento mayor que s, también tendremos que hay 1 tarea activa, porque se acumula a lo largo del árbol. La forma de contrarrestar esto, es insertar -1 en la posición e, para que no se propague el valor de la posición e en adelante. De esta manera, cuando consultemos el intervalo [s, e] tendremos 1 tarea activa, y si consultamos fuera del intervalo, tendremos 0.
Con esta idea, cada vez que tengamos una tarea, consultamos su inicio y su final en el BIT para saber si hay alguna ejecutándose en estos momentos, y si es así, tenemos un conflicto. De lo contrario, la insertamos en el árbol haciendo update(s, 1) y update(e, -1). Hay que tener cuidado especial con los puntos de inicio y final, ya que dos tareas si pueden «tocarse», pero no pueden solaparse.
